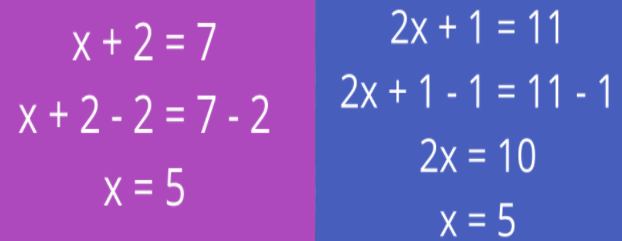Introduction to Algebra

History of Algebra:

A Persian Mathematician whose name was Muhammad ibn Musa Al-Khwarizmi (780-850 AD) is called the "Father Of Algebra. He wrote a book in the Arabic Language named Kitab Al Muhtasar fi Hisab Al Jabr-wal-Muqabala in 820 AD. Later on, it was translated into English named: The Compendious Book on Calculation by Completion and Balancing.  This book gives a step-wise solution for Linear and Quadratic Equations. Furthermore, He described the methods of solving different and complex Mathematical problems. 

                           The word ALGEBRA came from the Arabic word AL-Jabr which has its roots in a 9th-century codex written by Musa AL-Khwarizmi.

Algebra:

An Arabic word which means "Bringing together broken parts" is called Algebra. It is one of the useful tools of mathematics. It uses mathematical statements to describe the relationships between things that can vary with the  time. Furthermore, It is not only a mathematical concept but also a skill for all of us because we mostly use it in our daily life without even recognizing it. Moreover, It is also useful in all other topics of mathematics. Now, You are going to study this topic in future in a very easy way.

Different Branches of Algebra:

There are different branches of Algebra that we are going to study now to find the values of two or more variables. These branches are

1. Elementary Algebra
2. Advanced Algebra
3. Abstract Algebra
4. Linear Algebra
5. Communicative Algebra

1. Elementary Algebra

The branch of Algebra that deals with the study of some basic operations, concept of variables, and simplification of an algebraic expression with its evaluation and linear equations having one or two variables.

What is Algebra?

A branch of mathematics that deals with mathematical symbols and the Arithmetic operations in utilizing these mathematical symbols are called Algebra.

Relationship between Algebra and Arithmetic:

As, all of you already known about natural numbers (1,2,3,...) and the basic operations (+,₋,×,÷) in Arithmetic study. But in Algebra, We use letters/Alphabets (a, b, c,...,z) to add different numbers.

In the given figure, x+y=z is the general form of all above arithmetic statements. So, we can say that 

"Algebra is a general form of Arithmetic"

What is a Mathematical Statement?

A Mathematical statement is a sentence that will be either true or false.

Example:

• Faisalabad is in KPK.          (False)
• Mango is a fruit.                 (true)
• Thank you                           (Neither true nor false)

       But, the statements with mathematical symbols are

• ▢  + 2  = 4
• ∆  is a beautiful city.

Here ∆ and ▢ are unknown. In Algebra, we replace these unknown symbols by alphabetical letters like x, y, z etc.

How can you make any Mathematical statement True?

 

 A mathematical statement will become true by following the example given below:

Example:

 Algebraic Terms:  

 In order to write mathematical statements in algebra we use some basic terms which are given below:

• Coefficients
• Index or Exponential form
• Literals 
• Constant 
• Variables

Coefficients:

 A factor that is multiplied to a variable is called its coefficient.

Example:

      In 4x, 2y and 3z, the numbers 4, 2 and 3 are called coefficients.

Index or Exponential Form:

 In Mathematics, the index or exponent of any number means that how many times to multiply out the given number.

But in Algebra, the index or exponent tells us how many times to multiply out any variable.

Example:

 As, you know that

                             4×4×4=4³

 Here,3 is called the exponent of 3.

In algebraic form,

                           x× x ×x = x³

Literals:

           The letters or Alphabets that are used in mathematics to represent an unknown quantity are called literals or literal numbers.

We use literals in math without assigning any specific value at all.

Example:

The formula for Area of a square is given below:

i.e.                      Area = l × b

Here, L and b are called literals.

Constant:

In mathematics, any number that have fixed value is called constant.

Example:

       In x+3, the number 3 have fixed value is called constant.

Variables:

An unknown mathematical symbol which can take various numerical values and is not a constant, called variable.

Example:

         In x+3, x is called a variable.