In order to study subsets in mathematics, we deal with the pairs of sets. In these pairs of sets, the first set is contained inside the second set. Then the first set becomes the subset of the second set and the second set becomes the superset of the first set. Subsets are further divided into proper and improper subsets that we are going to study here:
Subsets:
Consider, there are any two sets M and N. If each element of set M is an element of set N then M is called a subset of N and denoted by M⊆N.
Always remember that:
“Every set is a subset of itself”
Example:
In the set of family members, Mother and Father are the subsets of the set of family members.
Our universe is very vast and has many things in it. Therefore,
The stars are the subsets of our universe.
The galaxies are the subsets of our universe.
The planets are the subsets of the Universe.
Examples of subsets in daily life:
Proper Subsets:
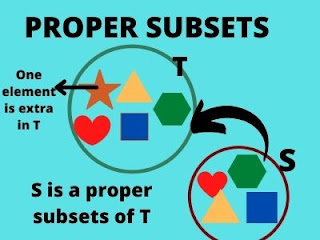
Any two sets M and N are called proper subsets if M is a subset of N but N is not a subset of M.
Additionally, If every element of set M is an element of sets IN but there occurs at least one element in N that is not an element of sets M then M is called the proper subset of N and is denoted by M⊂N.
Example:
If S = {11, 12, 13, 14, 15} and T = {12, 13}
Then T is a proper subset of S because S has more elements than T.
If R = { jhelum, chenab, ravi, beas, sutlej} and W = {chenab, ravi}
Here, W is a proper subset of R.
Examples of proper subsets in daily life:
Improper Subsets:
Improper subsets are slightly opposite to proper subsets. We can define as:
"Two sets M and N are called improper subsets if M is a subset of N and N is also a subset of M".
In other words, every element of set M is an element of N and each element of N is also an element of M then M and N are called improper subsets of each other and denoted by M⊆N.
Remember that
Improper subsets always have the same elements and are also called equal sets.
Examples:
If P = {cow, goat, dog} and G = {dog, cow, goat}
Then P and G are improper subsets because both have the same elements.
Suppose that E = {iqra, iman, ifra, irsa} and K = {ifra, isra, iman, iqra}
Then E and K are the improper subsets.
Examples of improper subsets in daily life:
Super Set:
For any two sets M and N, If M is a subset of N then N is called super set of M. Here, both M and N may have the same elements but all the elements of M must belong to N. Superset is denoted by ‘⊇’.
Example:
Let D = {1, 2, 3,...,9} and H = {2, 3}
Here H is called a subset of D and H is called the superset of D because D contains all the elements of H.
Assume that Y = {onion, radish, carrot, ladyfinger} and Z = {radish, carrot} then Y is a superset of Z.
Example of superset in daily life:
Power Sets:
A power set is a set that consists of all the subsets of any set under consideration. Let M be any set then its power set is denoted by P(M).
Example:
For any set D = {f, g, h} power sets are
P(D) = {∅, {f},{g},{h},{f, g},{f,h},{g,h},{f,g,h}} that have all the subsets of D.
Practice Questions
Question#1: Tell whether the following pair of sets are subsets or not?
(i) X = {f, g, h, a, e}, Y = {e, f, g}
(ii) U = {12,11, 15}, V = {11+0, 1+12, 3+12, 2+12, 1+11}
(iii) A = {6, 2, 8,0}, B = {8-2, 9-1, 6-2, 3-1, 2-2}
(iv) G = The set of prime numbers less than 11 , H = {7, 3, 2}
(v) F = {a, b, c,...,z}, Q = {g, h, f}
Question#2: If, X = {1, 2, 3}, Y = {1, 2, 3, 4, 5},and Z = {1, 4} then Whether the following statements are true or false?
(i) X ⊆ Y
(ii) X ⊇ Z
(iii) Y ⊇ Z
(iv) Z ⊆ X
(v) X ⊆ Z
(vi) Z ⊆ Y
Question#3: Deduce the power sets of the following.
(i) K = {x, y, z}
(ii) L= {4, 5}
(iii) M = {a, e}
(iv) N = (s, t, u, v)
(v) O = {$, %, &}